Question 1: 下列物理量属于矢量的是
下列物理量属于矢量的是
- A. A. 质量
- B. B. 速率
- C. C. 时间
- D. D. 摩擦力
Answer: D
下列物理量属于矢量的是
Answer: D
下列物理量中,属于矢量的是
Answer: B
运动员沿跑道的直道部分先向南跑了 50 m ,又折返向北跑了 30 m ,整个过程中,运动员的路程和位移大小分别是
Answer: A
关于质点的位移和路程,下列说法中正确的是
Answer: B
关于位移和路程的关系,下列说法正确的是
Answer: D
下列各组物理量中均为矢量的是
Answer: A
如图,物体沿两个半径为 $R$ 的半圆弧由 $A$ 运动到 $C$ ,则它的位移和路程分别是 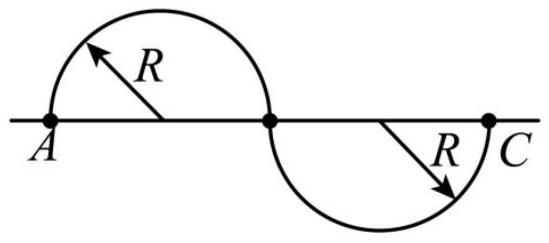
Answer: D
物体做直线运动时可以用坐标轴上的坐标表示物体的位置,用坐标的变化量表示物体的位移.如图所示,一个物体从 $C$ 运动到 $B$ 的位移是 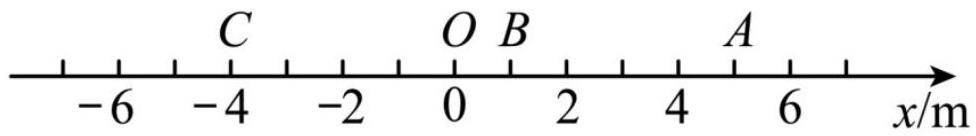
Answer: C
某平衡车性能测试过程速度随时间变化的 $v - t$ 图像如图所示,下列说法正确的是() 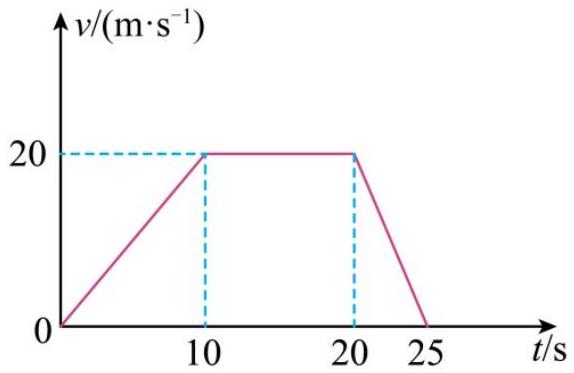
Answer: D
在平直公路上行驶的 $a$ 车和 $b$ 车,其位移时间图像分别为图中直线 $a$ 和曲线 $b . t = 3 \mathrm {~s}$ 时,直线 $a$ 和曲线 $b$ 刚好相切,下列说法正确的是 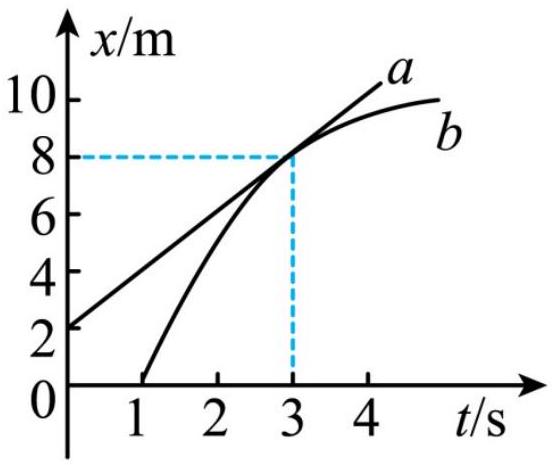
Answer: B
物体在月球表面的重力加速度是在地球表面的重力加速度的 $\frac { 1 } { 6 }$ ,这说明了
Answer: B
一个物体从静止开始做速度均匀变大的直线运动,它在第 4 s 末速度增大为 $4 \mathrm {~m} / \mathrm { s }$ ,则它的加速度为
Answer: B
一个物体从离地高 h 处自由落下,经过时间 t 落地,则它下落 $\mathrm { t } / 3$ 时间时,离地面的高度为( )
Answer: C
一个小石子从离地某一高度处由静止自由落下,某摄影爱好者拍到了它下落的一段轨迹,并测得该轨迹的实际长度为 20 cm .已知曝光时间为 $\frac { 1 } { 200 } \mathrm {~s}$ ,则小石子在拍摄前下落的距离约为
Answer: C
大小分别为 2 N 和 8 N 的两个力作用在一个质量为 2 kg 的物体上,则物体能获得的最小加速度和最大加速度分别是
Answer: A
物体沿着两个半径为 $R$ 的半圆弧由 $a$ 点运动到 $c$ 点,用时 $t$ ,如图所示,则它的平均速度和平均速率分别是 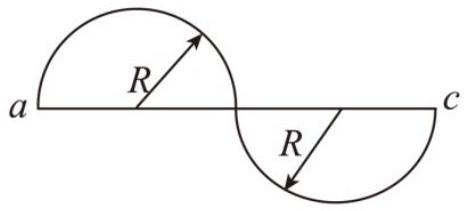
Answer: D
在一个美丽的中式园林中,存在一个独特的圆形景观区域,其半径为 20 m .这个区域中有一条别致的曲线通道,由两个半径均为 10 m 的半圆首尾相连构成.如图所示,一位游客在早晨 8 点从 $A$ 点出发,沿着图中箭头指示的曲线通道 $A O C$ 进行游览,并在 8 点 5 分到达 $C$ 点.设 $\pi = 3.14$ ,该游客从 $A$ 点到 $C$ 点的平均速度和平均速率分别约为 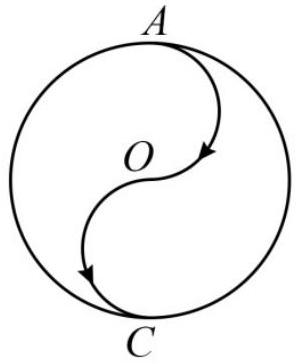
Answer: A
一个做直线运动的物体的 $v - t$ 图为如图所示的半圆,其在 $0 \sim 4 s$ 内的平均速度大小为 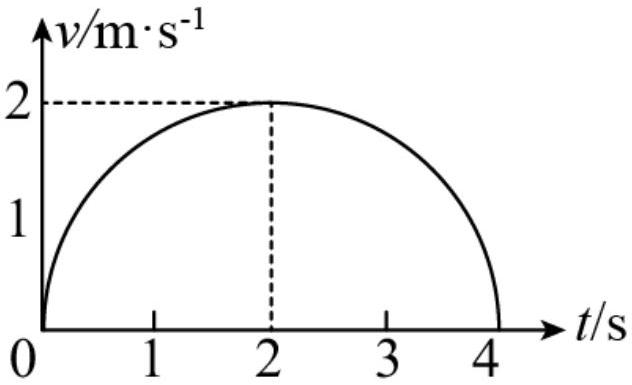
Answer: B
如图所示,屋檐上水滴下落的过程可以近似看成自由落体运动.假设水滴从离地 5 m高的屋檐上无初速度滴落,重力加速度 ${ } ^ { g = 10 \mathrm {~m} / \mathrm { s } ^ { 2 } }$ .则水滴下落到地面时的速度大小约为  水滴从屋檐自由下落
Answer: B
如图所示,在光滑水平面上,质量分别为 $m _ { \mathrm { A } } = 2 \mathrm {~kg} , m _ { \mathrm { B } } = 4 \mathrm {~kg}$ ,速度的大小分别为 $\nu _ { \mathrm { A } } = 5 \mathrm {~m} / \mathrm { s } , \nu _ { \mathrm { B } } = 2 \mathrm {~m} / \mathrm { s }$的 A,B 两小球沿同一直线相向运动并发生碰撞,则 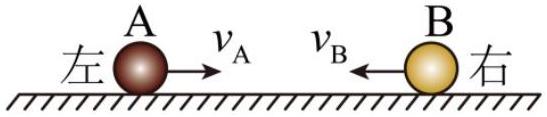
Answer: A
质量相等的 5 个物块在光滑水平面上间隔一定距离排成一直线,如图所示.具有初速度 $v _ { 0 }$ 的物块 1 向其他 4 个静止物块运动,依次发生碰撞,每次碰撞后不再分开.最后, 5 个物块粘成一整体,这个整体的速度等于 
Answer: C
如图所示,大小相同,质量分别为 0.2 kg 和 0.1 kg 的小球,在光滑水平面上分别以 $0.3 \mathrm {~m} / \mathrm { s }$ 和 $0.9 \mathrm {~m} / \mathrm { s }$ 的速度沿同一直线相向运动,相撞之后粘住成为一个整体,则整体的速度大小为 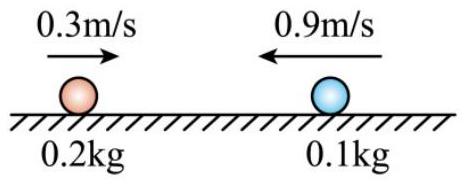
Answer: A
将一小球以 $10 \mathrm {~m} / \mathrm { s }$ 的速度水平抛出,经过 1 s 小球落地,不计空气阻力,$g$ 取 $10 \mathrm {~m} / \mathrm { s } ^ { 2 }$ 关 于这段时间小球的运动,下列表述正确的是
Answer: D
从距水平地面高 5 m 的位置,将小石块以某一速度水平抛出,落地时水平位移为 10 m . 不计空气阻力,取重力加速度 ${ } ^ { g = 10 \mathrm {~m} / \mathrm { s } ^ { 2 } }$ .则小石块
Answer: B
一个石子从 10 m 高的塔顶开始做自由落体运动,不计空气阻力,取 $g = 10 \mathrm {~m} / \mathrm { s } ^ { 2 }$ ,石子落地时的速度大小是
Answer: A
当一颗子弹以水平速度为 $3 v _ { 0 }$ ,恰好能射穿三块叠放在一起且坚直放置的相同的固定木板,那么当它刚射穿第一块板时,速度为
Answer: C
子弹的初速度为 $v$ ,打穿一块固定木板后的速度为零,要恰好打穿两块同样的固定木板,子弹的初速度应为
Answer: D
一子弹击中木板的速度是 $800 \mathrm {~m} / \mathrm { s }$ ,历时 0.02 s 穿出木板,穿出木板时的速度为 $300 \mathrm {~m} / \mathrm { s }$ ,则子弹穿过木板时的加速度为
Answer: B
倾角为 $37 ^ { \circ }$ 的斜面与水平面平滑连接,一滑块从斜面上某点由静止开始下滑,最后停在水平面上.已知滑块在斜面和水平面上滑行的距离相等,滑块与斜面和水平面间的动摩擦因数也相等, $\sin 37 ^ { \circ } = 0.6 , \cos 37 ^ { \circ } = 0.8$ ,则滑块与水平面间的动摩擦因数为
Answer: C
从 $t = 0$ 时刻起,一滑块在水平桌面上由静止开始沿直线运动,其加速度 $a$ 随时间 $t$ 变化的关系如图所示.已知 $t = 6 \mathrm {~s}$ 时,滑块的位移 $x = - 28 \mathrm {~m}$ .下列说法正确的是 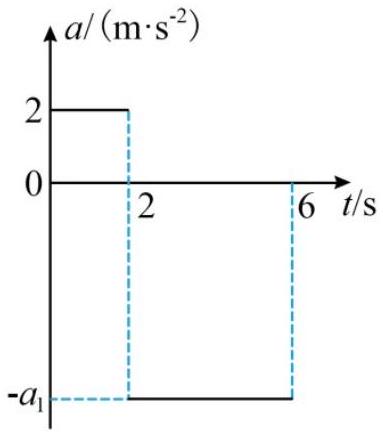
Answer: B
下列物理量中,属于矢量的是
Answer: B
一个运动员在 100 米赛跑中, 16 s 末到达终点时的瞬时速度为 $7.5 \mathrm {~m} / \mathrm { s }$ ,则全程内的平均速度的大小为
Answer: B
徐东海同学在汽车中观察速度计指针位置的变化.开始时汽车速度大小是 $36 \mathrm {~km} / \mathrm { h }$ ,经过 4 s 后速度大小是 $72 \mathrm {~km} / \mathrm { h }$ .若汽车运动过程中的加速度不变,则汽车的加速度为
Answer: A
一辆汽车在教练场上沿平直道路行驶,以 $x$ 表示它相对于出发点的位移.图示为汽车在 0 时刻到 40 s 这段时间的 $x - t$ 图像,下面说法正确的是 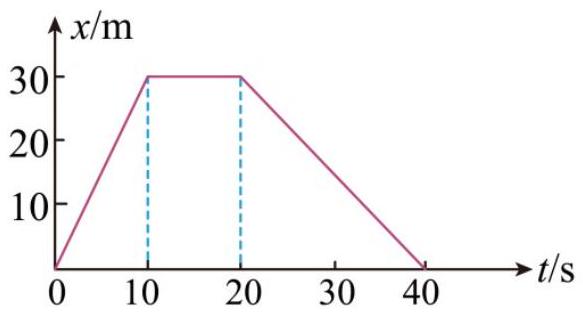
Answer: A
钢球由静止开始做自由落体运动,不计空气阻力,落地时的速度为 $30 \mathrm {~m} / \mathrm { s }$ ,则小球下落的平均速度为
Answer: B
假设航天员在月球上离月球表面高 10 m 处由静止释放一片羽毛,羽毛落到月球表面上的时间大约是(月球表面的重力加速度约为地球的 $\frac { 1 } { 6 }$ )
Answer: D
普通客机起飞的速度最低约为 $200 \mathrm {~km} / \mathrm { h }$ ,客机在跑道上做匀加速直线运动的加速度大小约为重力加速度大小的 $\frac { 1 } { 5 }$ ,则客机在跑道上的起飞距离最低约为
Answer: D
运动学
37 Practice Questions
The actual CSCA exam is available in Chinese and English
Кинематика описывает движение тел без учёта причин движения, включая равномерное и равноускоренное движение. На экзамене CSCA проверяется умение решать задачи на различные виды движения.
Правильно выбирайте систему координат и начало отсчёта времени, это упрощает решение задач.
Real exam: 48 questions mixing all topics, 60-minute limit, no hints. Many students find they can solve topics separately, but struggle when mixed.
Explore other subject practice: