Question 1: 两个阻值均为 $2 \Omega$ 的电阻串联后,总阻值为()
两个阻值均为 $2 \Omega$ 的电阻串联后,总阻值为()
- A. A. $3 \Omega$
- B. B. $4 \Omega$
- C. C. $5 \Omega$
- D. D. $6 \Omega$
Answer: B
两个阻值均为 $2 \Omega$ 的电阻串联后,总阻值为()
Answer: B
$1 \Omega , 2 \Omega , 3 \Omega$ 三个电阻并联后总阻值 $R$ 并为( )
Answer: D
将阻值均为 $2 R$ 的电阻进行并联后,总阻值为()
Answer: A
$20 \Omega$ 和 $30 \Omega$ 的两个电阻并联后,两端并联一条导线,那么这个电路的总阻值为( )
Answer: C
如图所示,电阻 $R _ { 1 } , R _ { 2 }$ 接入电路中,通过两电阻的电流相等,已知 $R _ { 1 } : R _ { 2 } = 1 : 2$ ,则 $U _ { 1 } : U _ { 2 }$ 为( ) 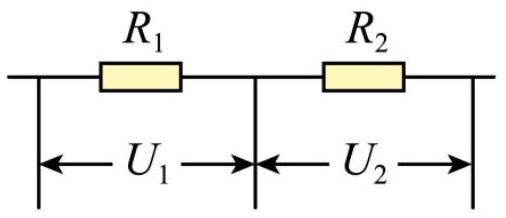
Answer: A
两电阻 $R _ { 1 } , R _ { 2 }$ 的电流 $I$ 和电压 $U$ 的关系如图所示,可知电阻大小之比 $R _ { 1 } : R _ { 2 }$ 等于( ) 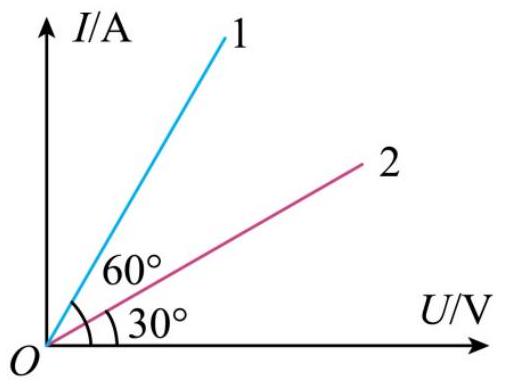
Answer: A
如图所示,电阻 $R _ { 1 } , R _ { 2 }$ 接入电路中,通过两电阻的电流相等,已知 $U _ { 1 } : U _ { 2 } = 1 : 2$ ,则 $R _ { 1 } : R _ { 2 }$ 为( ) 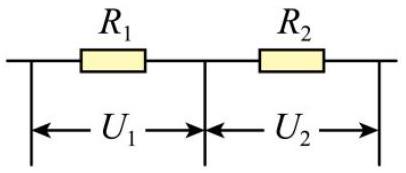
Answer: A
如图所示,图线 $a , b$ 分别表示电阻 $R _ { 1 } , R _ { 2 }$ 的伏安特性曲线,下列说法中正确的是( ) 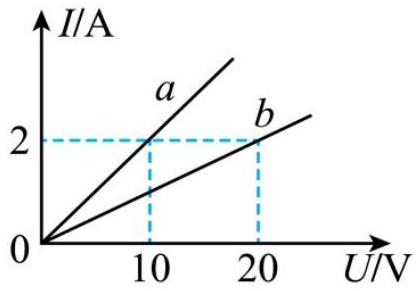
Answer: D
一个定值电阻,两端电压为 2 V ,通过的电流是 0.5 A ,如果两端的电压是 6 V ,通过的电流是( )
Answer: C
已知通过三个并联支路的电流之比是 $I _ { 1 } : I _ { 2 } : I _ { 3 } = 1 : 2 : 3$ ,则三个并联支路的电压之比 $U _ { 1 } : U _ { 2 } : U _ { 3 }$ 为( )
Answer: B
在电阻为 $4 \Omega$ 的导体中通以恒定电流, 5 s 内通过导体横截面的电荷量是 10 C ,这时加在导体两端的电压是()
Answer: A
有两个电阻,$R _ { 1 } = 2 \Omega , R _ { 2 } = 3 \Omega$ ,现把它们并联起来接入电路,则通过它们的电流之 比 ${ } ^ { I _ { 1 } : I _ { 2 } }$ 为( )
Answer: C
已知 $R _ { 2 } = R _ { 3 } , R _ { 1 }$ 未知,把它们接成图示电路,则它们的电流之比 $I _ { 1 } : I _ { 2 } : I _ { 3 }$ 等于( ) 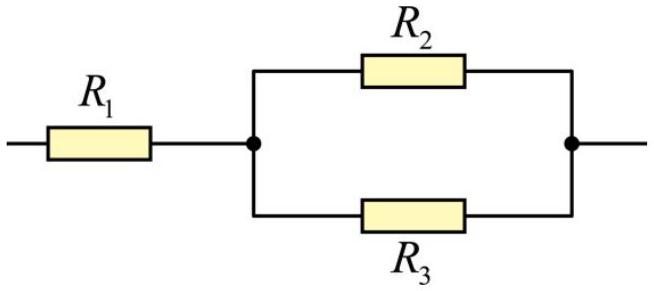
Answer: D
开关闭合后,将电压表接 $A , B$ 端显示 6 V ,将电压表接 $A , C$ 端显示 2 V ,则 $\mathrm { L } _ { 1 } , \mathrm {~L} _ { 2 }$ 两灯泡电阻之比 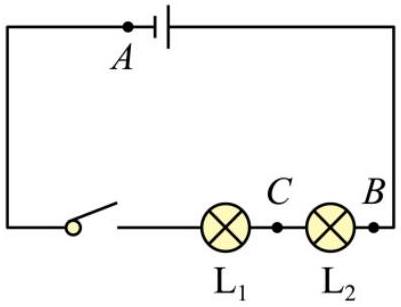
Answer: C
如图,电阻 $R _ { 1 } , R _ { 2 }$ 串联在电路中,已知 $R _ { 1 } = 1 \Omega , R _ { 2 } = 2 \Omega , R _ { 1 } , R _ { 2 }$ ,两端的电压分别为 $U _ { 1 } , U _ { 2 }$ ,通过的电流分别为 $I _ { 1 } , I _ { 2 }$ ,则 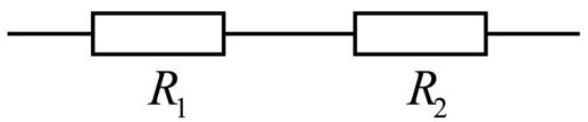
Answer: A
如图的理想电流表和理想电压表的示数分别是 0.2 A 和 0.4 V .此时小灯泡的电阻为( ) 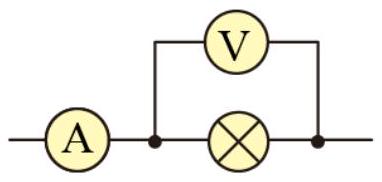
Answer: D
$R _ { 1 }$ 与 $R _ { 2 }$ 并联在电路中,通过 $R _ { 1 }$ 与 $R _ { 2 }$ 的电流之比为 $2 : 1$ ,则当 $R _ { 1 }$ 与 $R _ { 2 }$ 串联后接入电路中时,$R _ { 1 }$ 和 $R _ { 2 }$ 两端电压之比 $U _ { 1 } : U _ { 2 }$ 为( )
Answer: A
电源,电阻箱,电压表与开关连接成如图所示的电路.闭合开关 S 后,电压表示数为 2.00 V .当电阻箱接入电路的阻值 $R = 2.0 \Omega$ 时,通过电阻箱的电流 $I$ 为() 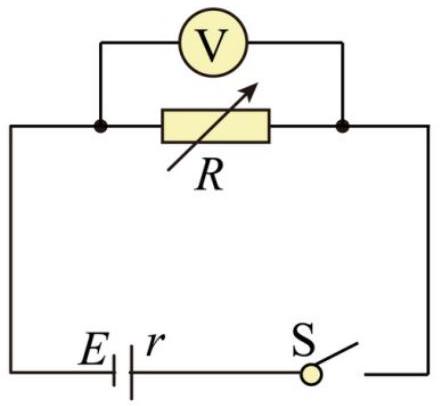
Answer: B
电压的单位是
Answer: C
下列是欧姆定律表达式的是
Answer: A
一根粗细均匀,阻值为 $16 \Omega$ 的电阻丝,保持温度不变,若先将它等分成 4 段,每段电阻为 $R _ { 1 }$ ,再将这 4 段电阻丝并联,并联后总电阻为 $R _ { 2 }$ ,则 $R _ { 1 }$ 与 $R _ { 2 }$ 的大小依次为
Answer: B
有三个电阻,$R _ { 1 } = 2 \Omega , R _ { 2 } = 3 \Omega , R _ { 3 } = 4 \Omega$ .现把它们串联起来接入电路中,则通过它们的电流之比 $I _ { 1 } : I _ { 2 } : I _ { 3 }$ 是
Answer: B
两电阻分别为 $6 \Omega$ 与 $8 \Omega$ ,并联后的总电阻为
Answer: D
如图所示的电路中,$R _ { 1 } = 1 \Omega , R _ { 2 } = 2 \Omega , R _ { 3 } = 3 \Omega$ ,闭合开关,那么通过电阻 $R _ { 1 } , R _ { 2 }$ , $R _ { 3 }$ 的电流之比 $I _ { 1 } : I _ { 2 } : I _ { 3 }$ 为 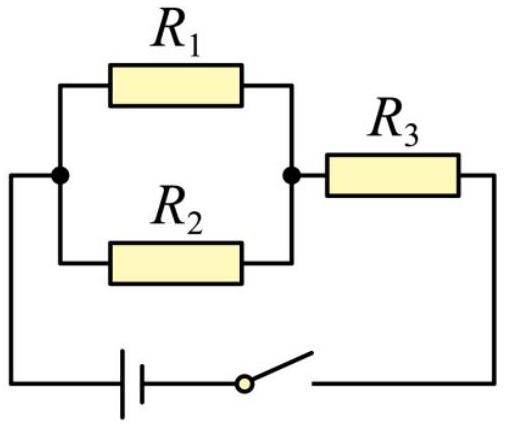
Answer: C
如图所示电路中,电阻 $R _ { 1 } , R _ { 2 } , R _ { 3 }$ 的阻值相同,将 $a , b$ 分别接到电源两端,则 $R _ { 1 }$ 与 $R _ { 3 }$ 的电压之比为 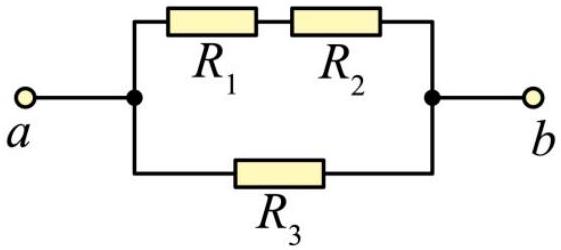
Answer: B
有两个电阻,$R _ { 1 } = 2 \Omega , R _ { 2 } = 3 \Omega$ ,现把它们串联起来接入电路,则通过它们的电流之 比 ${ } ^ { I _ { 1 } : I _ { 2 } }$ 为
Answer: A
两个相同的电阻串联起来的总电阻为 $12 \Omega$ ,则将它们并联起来的总电阻为
Answer: A
一个标有" 6 V 0.5 A "的灯泡,如果把它接在 10 V 的电源上,应连接一个阻值为几 $\Omega$ 的电阻,才能正常发光
Answer: A
三个阻值分别为 $4 \Omega , 6 \Omega , 12 \Omega$ 的电阻,以不同方式进行组合连接,获得的总电阻的最大值和最小值分别为
Answer: B
如图所示,电阻 $R _ { 1 } , R _ { 2 }$ 串联接入电路,已知 $R _ { 1 } : R _ { 2 } = 1 : 2$ ,则 $U _ { 1 } : U _ { 2 }$ 为 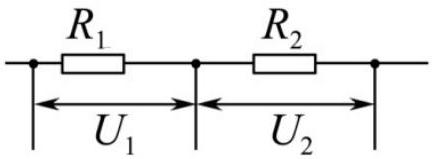
Answer: B
如图,电阻 $R _ { 1 } , R _ { 2 }$ 串联接入电路,已知 $U _ { 1 } : U _ { 2 } = 1 : 2$ ,则 $R _ { 1 } : R _ { 2 }$ 为() 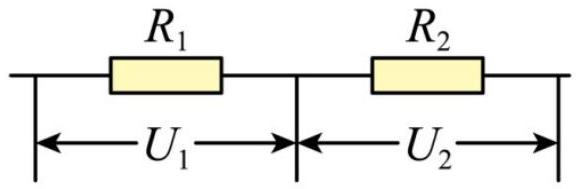
Answer: A
已知 $R _ { 1 } = R _ { 2 } , R _ { 3 }$ 未知把它们接成图示电路,求它们的电流 $I _ { 1 } I ^ { I _ { 2 } } : I _ { 3 }$ 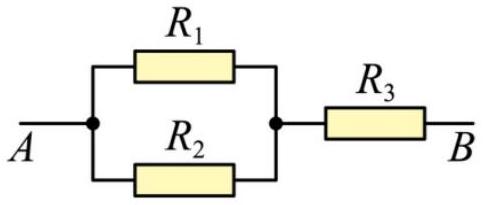
Answer: A
如图所示,$A B$ 两端接直流稳压电源,$U _ { A B } = 100 \mathrm {~V} , R _ { 0 } = 40 \Omega$ ,滑动变阻器总电阻 $R = 20 \Omega$ ,当滑动片处于变阻器中点时,$C , D$ 两端电压 $U _ { C D }$ 为( ) 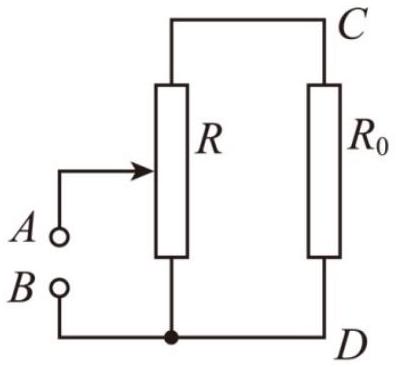
Answer: B
已知通过三个并联支路的电流之比 $I _ { 1 } : I _ { 2 } : I _ { 3 } = 1 : 2 : 3$ ,则三个并联支路的电阻之比 $R _ { 1 } : R _ { 2 } : R _ { 3 }$为
Answer: A
一个定值电阻,两端电压为 2 V ,通过的电流是 0.5 A ,如果两端的电压是 6 V ,要测量流 过的电流,电流表的量程可选用(
Answer: C
A 【知识点】计算电阻串联或并联时的电压,电流和电阻 【详解】三个并联支路的电压相等,根据欧姆定律 $U = I R$ 得,电流 $I$ 与电阻 $R$ 成反比.电流之比 $I _ { 1 } : I _ { 2 } : I _ { 3 } = 1 : 2 : 3$ ,则电阻之比 $$ R _ { 1 } : R _ { 2 } : R _ { 3 } = 6 : 3 : 2 $$
Answer: A
直流电路
36 Practice Questions
The actual CSCA exam is available in Chinese and English
Цепи постоянного тока изучают законы Ома, соединения резисторов и расчёт электрических цепей. На экзамене CSCA проверяется умение анализировать схемы и рассчитывать токи, напряжения и мощность.
Систематически применяйте правила Кирхгофа для сложных цепей и проверяйте ответы через баланс мощностей.
Real exam: 48 questions mixing all topics, 60-minute limit, no hints. Many students find they can solve topics separately, but struggle when mixed.
Explore other subject practice: