Question 1: 角速度反映了物体做匀速圆周运动的快慢,下列表达式中角速度的定义式是
角速度反映了物体做匀速圆周运动的快慢,下列表达式中角速度的定义式是
- A. A. $\omega = \frac { v } { R }$
- B. B. $\omega = \frac { 2 \pi } { T }$
- C. C. $\omega = \frac { \varphi } { t }$
- D. D. $\omega = 2 \pi n$
Answer: C
角速度反映了物体做匀速圆周运动的快慢,下列表达式中角速度的定义式是
Answer: C
一质点做匀速圆周运动,其线速度大小为 $4 \mathrm {~m} / \mathrm { s }$ ,转动周期为 2 s ,下列说法不正确的是
Answer: A
一个电子钟的秒针角速度为
Answer: C
如图,一质量为 20 kg 的小朋友乘坐摩天轮,随座舱做匀速圆周运动.若小朋友做圆周运动的半径为 50 m ,角速度为 $0.2 \mathrm { rad } / \mathrm { s }$ ,则小朋友所需的向心力大小为 
Answer: C
一个质点沿半径为 $r$ 的圆做匀速圆周运动,线速度为 $v$ ,则它的角速度是
Answer: C
如图所示,一质点花了 20 s 的时间沿圆形轨道从 $A$ 点运动到 $B$ 点,质点与圆心的连线在这段时间内转过的角度为 $\frac { \pi } { 3 }$ ,该过程中质点可以看成做匀速圆周运动,质点的角速度为( ) 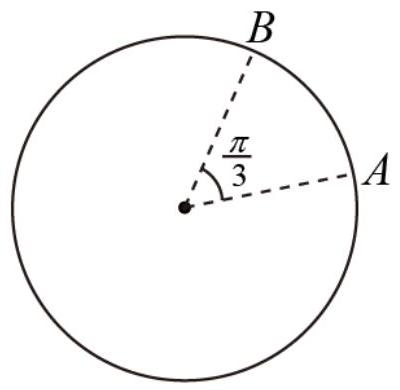
Answer: D
下列物理量属于矢量且单位符号表示正确的是
Answer: A
一质点做匀速圆周运动,其线速度大小为 $4 \mathrm {~m} / \mathrm { s }$ ,转动半径为 2 m ,那么
Answer: C
一小球以 $8 \mathrm {~m} / \mathrm { s } ^ { 2 }$ 的向心加速度做匀速圆周运动,半径为 2 m ,则小球运动的线速度大小为
Answer: B
如图所示,水平圆台转动的角速度 ${ } ^ { \omega = 0.6 \mathrm { rad } / \mathrm { s } \text { ,质量为 } { } ^ { 0.2 \mathrm {~kg} } \text { 的小物块 } A \text { 放在距离轴 } }$心 1 m 处与圆台相对静止一起转动,小物块受到的静摩擦力大小为 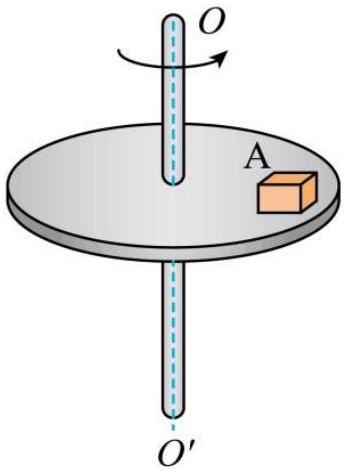
Answer: A
质量相等的 A , B 两物体置于绕坚直轴匀速转动的水平圆盘上, A 与转轴的距离是 B与转轴距离的 2 倍,且始终相对于圆盘静止,则两物体 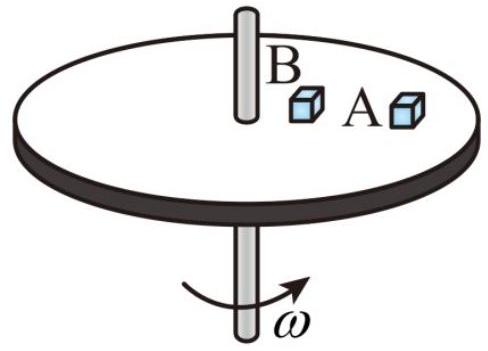
Answer: B
两个质量相等的球形物体,两球心相距 $r$ ,它们之间的万有引力为 $F$ ,若它们的质量不变,两球心的距离增大到原来的 2 倍,它们之间的作用力为
Answer: C
关于万有引力公式正确的是
Answer: B
地球质量大约是月球质量的 81 倍,一个飞行器在地球与月球之间.当地球对它的引力和月球对它的引力大小相等时,该飞行器距地心的距离与距月心的距离之比为
Answer: D
引力常量 $G$ 约等于
Answer: D
已知地球质量为某行星质量的 144 倍,地球半径为该行星半径的 3 倍,忽略星球自转,一辆车在地球表面所受地球引力为 1600 N ,则其在该行星表面所受引力为
Answer: C
如图所示,两个质量分布均匀的实心球,半径分别为 $r _ { 1 } = 0.4 \mathrm {~m} , r _ { 2 } = 0.6 \mathrm {~m}$ ,质量分别为 $m _ { 1 } = 4.0 \mathrm {~kg} , m _ { 2 } = 1.0 \mathrm {~kg}$ ,两球间距离为 $r = 2.0 \mathrm {~m}$ ,则两球间相互引力的大小为 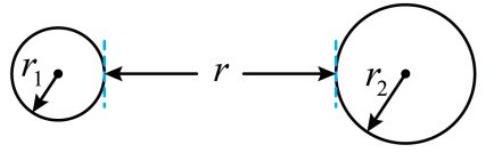
Answer: C
一质量 $m = 1 \mathrm {~kg}$ 的物体在坚直面内做半径 $R = 1 \mathrm {~m}$ 的匀速圆周运动,从最低点运动到最高 点,速度变化量的大小为 $4 \mathrm {~m} / \mathrm { s }$ ,则物体做圆周运动的向心力大小为
Answer: A
某质点做匀速圆周运动,转动半径 $r = 2 \mathrm {~m}$ ,角速度 $\omega = \pi \mathrm { rad } / \mathrm { s }$ .若其角速度增大为 $2 \pi \mathrm { rad } / \mathrm { s }$ ,半径不变,则线速度大小的变化量为
Answer: B
如图所示,小球在细绳牵引下,在水平光滑桌面上以角速度 $\omega$ 做半径为 $r$ 的匀速圆周运动,小球的线速度大小为 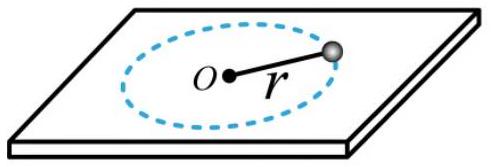
Answer: C
圆周运动与万有引力
20 Practice Questions
The actual CSCA exam is available in Chinese and English
Круговое движение описывает движение тел по окружности, включая центростремительное ускорение и силы. На экзамене CSCA проверяется применение законов кругового движения к различным физическим ситуациям.
Всегда определяйте, какая сила обеспечивает центростремительное ускорение, и правильно выбирайте систему отсчёта.
Real exam: 48 questions mixing all topics, 60-minute limit, no hints. Many students find they can solve topics separately, but struggle when mixed.
Explore other subject practice: