Question 1: 一个盒子内有 150 粒绿豆和 200 粒红豆,从盒子内随机取一粒豆子,则所取豆子为红豆的概率为()
一个盒子内有 150 粒绿豆和 200 粒红豆,从盒子内随机取一粒豆子,则所取豆子为红豆的概率为()
- A. A. $\frac { 3 } { 7 }$
- B. B. $\frac { 18 } { 35 }$
- C. C. $\frac { 4 } { 7 }$
- D. D. $\frac { 3 } { 5 }$
Answer: C
一个盒子内有 150 粒绿豆和 200 粒红豆,从盒子内随机取一粒豆子,则所取豆子为红豆的概率为()
Answer: C
从 $1,2,3,4,5$ 这五个数中随机抽取两个不同数字,则这两个数字乘积为偶数,且它们的积大于 11 的概率为( )
Answer: C
某同学抛掷一枚质地均匀的硬币,连续抛掷 10 次,都是反面朝上,则第 11 次正面朝上的概率是()
Answer: B
掷一颗质地均匀的正方体骰子,出现点数是 1 的概率是( )
Answer: A
一个不透明的袋子里装有 4 个白球和 3 个黑球,这些球除颜色外完全相同.从袋子中随机摸出一个球,则摸到白球的概率是( )
Answer: A
从长度为 $1,3,5,7,9$ 的 5 条线段中任取 3 条,则这三条线段能构成一个三角形的概率为( )
Answer: C
已知随机变量 $X$ 满足 $E ( 2 - 2 X ) = 4 , D ( 2 - 2 X ) = 4$ ,下列说法正确的是( )
Answer: D
若随机变量 $X$ 满足 $D ( X ) = 4$ ,则 $\sigma ( 3 X - 2 ) =$( )
Answer: C
已知离散型随机变量 $X$ 的方差为 1 ,则 $D ( 2 X - 1 ) =$( )
Answer: D
若数据 ${ } ^ { X _ { 1 } } , ~ { } ^ { X _ { 2 } } , \cdots , { } ^ { X _ { n } }$ 的方差为 1 ,则数据 ${ } ^ { 3 x _ { 1 } - 1 } , ~ 3 x _ { 2 } - 1 , \cdots , ~ 3 x _ { n } - 1$ 的方差为
Answer: D
若随机变量 $X$ 满足 $D ( X ) = 9$ ,则 $D ( 2 X + 3 ) =$( )
Answer: D
已知一组数据 ${ } ^ { X _ { 1 } } , { } ^ { X _ { 2 } } , \cdots , { } ^ { X _ { 7 } }$ 的方差为 3 ,则数据 ${ } ^ { 2 X _ { 1 } + 1 } , ~ { } ^ { 2 X _ { 2 } + 1 } , \cdots , ~ { } ^ { 2 X _ { 7 } + 1 }$ 的方差为( )
Answer: C
在篮球比赛中,罚球命中 1 次得 1 分,不中得 0 分.如果某运动员罚球命中的概率为 0.8.那么他罚球 1 次的得分 $X$ 的均值是( )
Answer: B
已知随机变量 $X \sim N ( 0,1 )$ 且 $P ( - 2 \leq X \leq 2 ) = 0.9545$ ,则 $P ( X > 2 ) =$
Answer: C
已知随机变量 $X \sim N \left( - 1 , \sigma ^ { 2 } \right)$ ,且 $P ( X \leq 1 ) = 0.65$ ,则 $P ( X < - 3 ) =$( )
Answer: A
已知随机变量 $X$ 服从正态分布 $N \left( 4 , \sigma ^ { 2 } \right)$ ,若 $P ( X < 1 + 2 a ) = P ( X > 1 - a )$ ,则 $a =$
Answer: D
若随机变量 ${ } ^ { X \sim N \left( 1 , \sigma ^ { 2 } \right) }$ ,且 $P ( X \leq a ) = P ( X \geq b )$ ,则 $a + b$ 的值为( )
Answer: C
若随机变量 $X \sim N ( 6,8 )$ ,则当 $P ( X < a - 2 ) = P ( X > 5 )$ 时,$a$ 的值为( )
Answer: A
已知随机变量 $X$ 服从正态分布 $N \left( 3 , \sigma ^ { 2 } \right) , P ( X \leq 4 ) = 0.84$ ,则 $P ( 2 < X \leq 4 ) =$()
Answer: C
从11,12,13,L ,30中任意选一个数,则这个数是奇数或能被 3 整除的概率为
Answer: D
将一枚质地均匀的硬币连掷 4 次,出现"至少两次正面向上"的概率为
Answer: D
已知 5 件产品中有 2 件次品,其余为合格品,现从这 5 件产品中任取 2 件, 2 件都是合格品的概率为( )
Answer: A
从 $a , b , c , d$ 四个字母中,随机抽取一个字母,则抽到字母 $a$ 的概率是( )
Answer: A
同时掷两枚骰子,向上点数和为 6 的概率是()
Answer: C
某兴趣小组有 2 名男生和 3 名女生,现从中任选 2 名学生去参加活动,则恰好选中 2名女生的概率为( )
Answer: C
在袋中有编号依次为 $1,2,3 , \cdots , 10$ 的 10 小球,先从袋中随机摸取一个小球,则摸得的是 小球编号是 3 的倍数的概率是( )
Answer: C
中国古代传统文化中,有记录人们出生年份的属相记录法,共有 12 种属相,分别是鼠,牛,虎,兔,龙,蛇,马,羊,猴,鸡,狗,猪,也称子,丑,寅,卯,辰,巳,午,未,申,酉,戊,亥,现有一个正十二面体,每一个(正五边形)面标有一个属相,如图.现将这个质地均匀的正十 二面体先后抛掷两次,则朝上的面两次属相不同的概率是 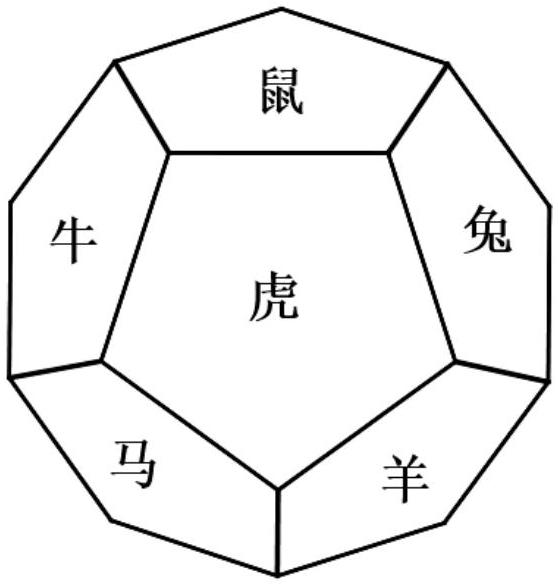
Answer: B
抛掷一枚骰子得到偶数点的概率是
Answer: D
将3枚硬币随机抛出,其中恰好两个正面向上的概率为
Answer: B
现有 6 张牌面分别是 $2,3,4,5,6,7$ 的扑克牌,从中取出 1 张,记下牌面上的数字后放回,再取一张记下牌面上的数字,则两次所记数字之和能整除 18 的概率是
Answer: D
袋中装有 6 个白球, 5 个黄球, 4 个红球,从中任取一球,取到白球的概率为
Answer: A
袋中有 2 个白球, 2 个黑球,若从中任意摸出 2 个,则至少摸出 1 个黑球的概率是
Answer: D
抛掷一枚硬币两次,则至少有一次正面朝上的概率是
Answer: D
为弘扬我国古代"六艺"文化,某校研学活动社团计划开设"礼,乐,射,御,书,数"六门体验课程.若甲,乙两位同学均只能体验其中一门课程,则甲,乙恰好选中相同课程的概率为( )
Answer: D
从一副 52 张的扑克牌中任抽一张,"抽到 $K$ 或 $Q$"的概率是()
Answer: D
盒子里有 4 个白球和 5 个黑球,从中任取一个,取出白球的概率是
Answer: B
中国农历的"二十四节气",凝结着中华民族的智慧,是中国传统文化的结晶,如五月有立夏,小满,六月有芒种,夏至,七月有小暑,大暑.现从五月,六月,七月这六个节气中任选两个节气,则这两个节气恰在同一个月的概率为( )
Answer: A
口袋中有 100 个大小相同的红球,白球,黑球,其中红球 45 个,从口袋中摸出一个球,摸出白球的概率为 0.23 ,则摸出黑球的概率为( ).
Answer: A
掷一枚质地均匀的硬币正面朝上的概率是()
Answer: B
袋中装有除颜色外其他均相同的 4 个白球, 2 个黄球, 3 个红球,从中任取一球,则取到红球的概率为( )
Answer: C
概率与统计
40 Practice Questions
The actual CSCA exam is available in Chinese and English
Теория вероятностей и статистика изучают случайные события и методы анализа данных. На экзамене CSCA проверяется расчёт вероятностей и понимание основных статистических понятий.
Внимательно определяйте, являются ли события совместными или независимыми, прежде чем применять формулы.
Real exam: 48 questions mixing all topics, 60-minute limit, no hints. Many students find they can solve topics separately, but struggle when mixed.
Explore other subject practice: